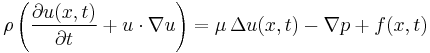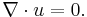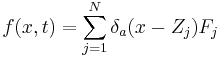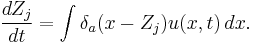Immersed boundary method
The immersed boundary method is an approach – in computational fluid dynamics – to model and simulate mechanical systems in which elastic structures (or membranes) interact with fluid flows. Treating the coupling (the elastic boundary changes the flow of the fluid and the fluid moves the elastic boundary simultaneously) of the structure deformations and the fluid flow poses a number of challenging problems for numerical simulations. In the immersed boundary method approach the fluid is represented in an Eulerian coordinate frame and the structures in a Lagrangian coordinate frame. For Newtonian fluids governed by the Navier–Stokes equations the immersed boundary method fluid equations are
with incompressibility condition
The immersed structures are typically represented by a collection of interacting particles 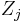 with a prescribed force law, where
with a prescribed force law, where 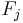 is the force acting on the
is the force acting on the 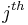 particle. The forces are accounted for in the fluid equations by the force density
particle. The forces are accounted for in the fluid equations by the force density
where 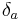 is an approximation of the Dirac
is an approximation of the Dirac 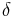 -function smoothed out over a length scale
-function smoothed out over a length scale  . The immersed structures are then updated using the equation
. The immersed structures are then updated using the equation
Variants of this basic approach have been applied to simulate a wide variety of mechanical systems involving elastic structures which interact with fluid flows. See the references for more details.
See also
References
- C. S. Peskin, The immersed boundary method, Acta Numerica, 11, pp. 1–39, 2002.
- C.S. Peskin, Numerical analysis of blood flow in the heart, J. Comput. Phys. 25 (1977) 220–252.
- R. Mittal and G. Iaccarino, Immersed Boundary Methods, Annual Review of Fluid Mechanics, vol. 37, pp. 239–261, 2005.
- Y. Mori and C. S. Peskin, Implicit Second Order Immersed Boundary Methods with Boundary Mass Computational Methods in Applied Mechanics and Engineering, 2007.
- L. Zhua and C. S. Peskin, Simulation of a flapping flexible filament in a flowing soap film by the immersed boundary method, Journal of Computational Physics, vol. 179, Issue 2, pp. 452–468, 2002.
- P. J. Atzberger, P. R. Kramer, and C. S. Peskin, A Stochastic Immersed Boundary Method for Fluid-Structure Dynamics at Microscopic Length Scales, Journal of Computational Physics, vol. 224, Issue 2, 2007. [DOI] .
- A. M. Roma, C. S. Peskin, and M. J. Berger, An adaptive version of the immersed boundary method, Journal of Computational Physics, vol. 153 n.2, pp. 509–534, 1999.
- Jindal S. et al. “The Immersed Boundary CFD Approach for Complex Aerodynamics Flow Predictions” SAE Journal, Detroit, Michigan 2007-01-0109 (2007)